Definición y Compatibilidad de los Sistemas de Ecuaciones

Definición

✅Se conoce como ecuación a un enunciado matemático que afirma la existencia de una igualdad entre dos cantidades en las cuales intervienen parámetros desconocidos a los que se les denomina incógnitas que se representan por letras. 

✅Teniendo un conjunto de ecuaciones con variables similares y relativas entre sí, es posible construir un sistema de ecuaciones cuya representación viene dada por los coeficientes, incógnitas y términos independientes de las ecuaciones planteadas. Sabiendo entonces que un sistema de ecuaciones de tipo lineal es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.

Compatibilidad de los Sistemas de Ecuaciones

✅Desde el punto de vista algebraico podemos averiguar si un sistema es o no compatible mediante el Teorema de Rouché-Frobenius que depende del valor común entre el rango de matrices lineales y el número de variables para determinar la compatibilidad o incompatibilidad del sistema.

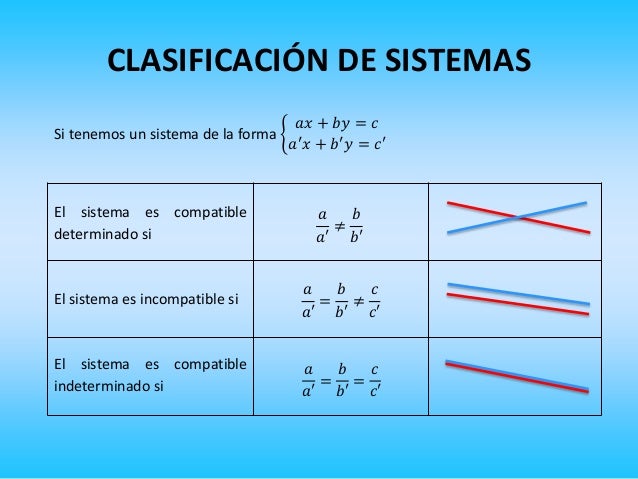
Fíjate en esta imagen y respondes:

Les compartimos un video sencillo para reconocer la Compatibilidad de los Sistemas de Ecuaciones

Referencias Bibliográficas:
💬Academia Internet (2013) Sistemas de Ecuaciones: Compatible Determinado, Compatible Indeterminado, Incompatible. (video) YouTube. Obtenido de: https://www.youtube.com/watch?v=Y_whRATbTSg
💬Wikipedia (2021) Sistema de ecuaciones algebraicas. Obtenido de: https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_algebraicas

💬 Descarte 2D (s.f.) Ecuaciones lineales: Compatibilidad de un sistema de ecuaciones lineales. Obtenido de: http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_ecuaciones_lineales_lrm/compatibilidad.htm