Método de la Matriz Inversa para solucionar un Sistema de Ecuaciones

 

✅Supongamos que tenemos un sistema de $n$ ecuaciones lineales con $n$ incógnitas. Podemos representar el sistema de forma matricial como 

1. La matriz $A$ es de dimensión $nxn$ y contiene en cada fila los coeficientes de las incógnitas de cada ecuación.
2. La matriz $x$ es de dimensión $nx1$ (una columna) y contiene las $n$ incógnitas del sistema.
3. La matriz $b$ es de dimensión $nx1$ y contiene los términos independientes de las ecuaciones.

✅Si el sistema tiene una única solución (es compatible determinado), entonces la matriz 

$A$ es regular (determinante distinto de 0) y, por tanto, existe su matriz inversa $A^{-1}$.

✅Entonces, podemos multiplicar toda la ecuación por la inversa de $A^{-1}$:

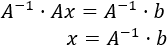
✅Es decir, si la matriz $A$ es regular, entonces la matriz columna resultante del producto matricial $A^{-1}\cdot b$ contiene la solución del sistema $Ax=b$.

👀👀👀Veamos el siguiente ejemplo:

Sistema de 3 ecuaciones con 3 incógnitas (3x3)

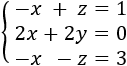
La matriz de coeficientes del sistema será:

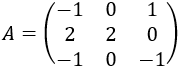
Es una matriz regular porque su determinante es 4. Su inversa será:

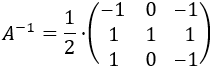
La matriz de términos independientes del sistema es

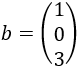
Calculamos la solución del sistema multiplicando las matrices $A^{-1}$ y $b$:

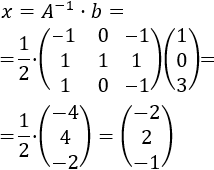
Por tanto, la solución del sistema es

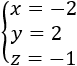
Aquí les dejamos un video para que se apoyen: