Regla de Cramer para solucionar un Sistema de Ecuaciones

✅Sirve para resolver sistemas de ecuaciones lineales que cumplan las condiciones siguientes:

1. El numero de ecuaciones es igual al numero de incógnitas
2. El determinante de la matriz de los coeficientes es distinto de cero

✅Es por definición, compatible determinado, puesto que se cumple que el rango (A) = rango (A*) =N° (numero de incógnitas) 

    En tal sentido, se presenta el siguiente ejemplo:

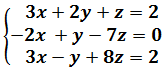
Calculamos el determinante de la matriz de coeficientes del sistema por la regla de Sarrus:

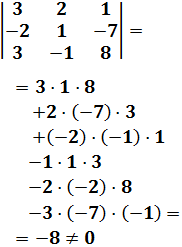
Como el determinante es distinto de 0, la matriz es regular y el sistema tiene una única solución (sistema compatible determinado):

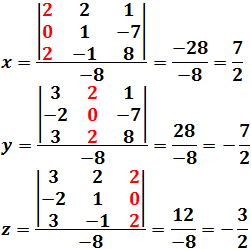
👀👀Nota: para calcular la incógnita asociada a la columna nn, sustituimos la columna nn de la matriz de coeficientes por la columna de términos independientes.

✅Aquí les dejamos un par de ejercicios resueltos para que estudies y practiques lo aprendido:

Referencias Bibliográficas:

💬S.A. (s.f) Regla de Cramer. Obtenido de: https://www.matesfacil.com/matrices/ecuaciones/sistemas-ecuaciones-matriciales-resueltas-ejemplos-matriz-inversa-solucion-problemas.html