Sistema Matricial de Ecuaciones: Teorema de Rouché-Frobenius

¿De una ecuación a una matriz?

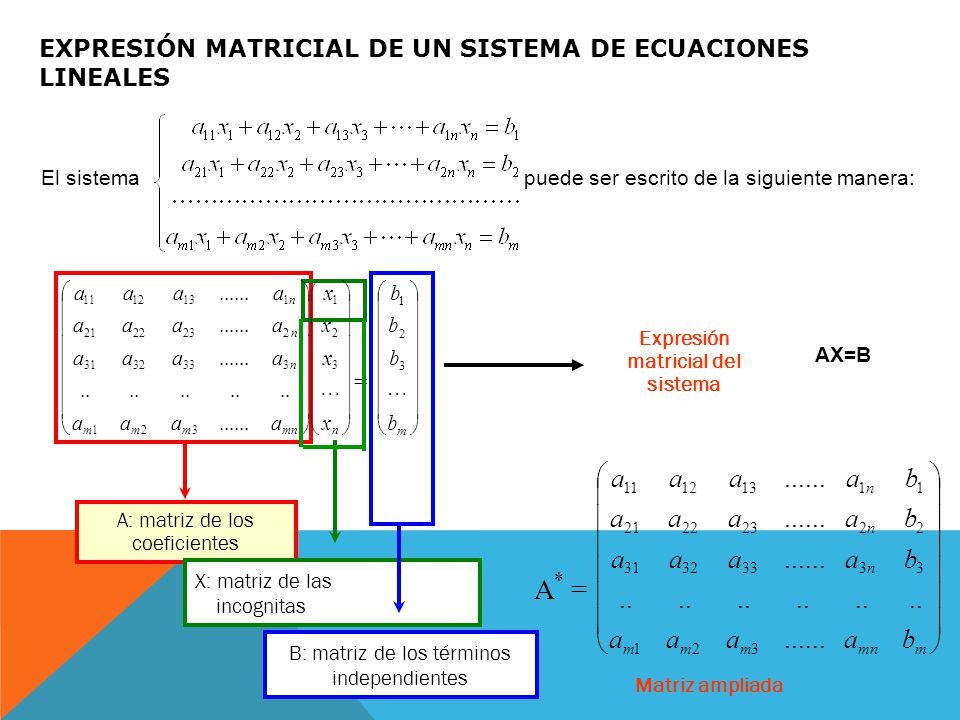
✅Del algebra lineal entendemos que cualquier sistema de ecuaciones lineales puede escribirse siempre en forma matricial a partir de sus incógnitas. Partiendo de un sistema con m ecuaciones lineales y n incógnitas cuyos coeficientes están en un cuerpo K (como números reales o complejos) se puede definir una matriz de coeficientes A, otra de incógnitas x; y otra de términos independientes b, que se representan de la forma A(x)=b.

La primera matriz está dada los coeficientes (A)
La segunda matriz está dada por las incógnitas (x)
La tercera matriz está dada por los términos independientes (b)

✅Ahora que conocemos el sistema matricial de ecuaciones podemos el enunciado del teorema debido al francés Eugene Rouché y al alemán Georg Ferdinand Frobenius se hace posible resolver cualquier tipo de sistemas de ecuaciones de primer grado, tenga o no solución, bajo el análisis del rango de matrices representativas del sistema.

✅La condición necesaria y suficiente para que un sistema de ecuaciones lineales sea compatible (tenga solución) es que el rango de la matriz de los coeficientes sea igual al rango de la matriz ampliada. Para esta resolución se discute el sistema bajo el rango de las matrices y se verifica sin la matriz de coeficiente y la ampliada son iguales que por tanto quiere decir que el sistema es compatible.

✅Si el número de incógnitas es igual al rango entonces será determinado (unas solución), y si el número de incógnitas es mayor al rango entonces el sistema es indeterminado y tiene soluciones infinitas. Cabe agregar que si los rangos de las matrices son distintos entonces existe incompatibilidad y no hay solución posible.

🔎🔎El enunciado del teorema es el siguiente🔍🔍

Existen soluciones para el sistema si y solo si el rango de la matriz completa es igual al rango de la matriz incompleta.
Entonces, si existen soluciones, estas forman un subespacio de $K^{n}$ de dimensiones $n-{\mbox{rg}}(A)$ . Si ${\mbox{rg}}(A)=n$ entonces la solución es única , de otro modo existen infinitas soluciones posibles.